Building with Patterns: The Approximation Pattern
March 14, 2019 | Updated: March 21, 2019
Imagine a fairly decent sized city of approximately 39,000 people. The exact number is pretty fluid as people move in and out of the city, babies are born, and people die. We could spend our days trying to get an exact number of residents each day. But most of the time that 39,000 number is "good enough." Similarly, in many applications we develop, knowing a "good enough" number is sufficient. If a "good enough" number is good enough then this is a great opportunity to put the Approximation Pattern to work in your schema design.
The Approximation Pattern
We can use the Approximation Pattern when we need to display calculations that are challenging or resource expensive (time, memory, CPU cycles) to calculate and for when precision isn't of the highest priority. Think again about the population question. What would the cost be to get an exact calculation of that number? Would, or could, it have changed since I started the calculation? What's the impact on the city's planning strategy if it's reported as 39,000 when in reality it's 39,012?
From an application standpoint, we could build in an approximation factor which would allow for fewer writes to the database and still provide statistically valid numbers. For example, let's say that our city planning strategy is based on needing one fire engine per 10,000 people. 100 people might seem to be a good "update" period for planning. "We're getting close to the next threshold, better start budgeting."
In an application then, instead of updating the population in the database with every change, we could build in a counter and only update by 100, 1% of the time. Our writes are significantly reduced here, in this example by 99%. Another option might be to have a function that returns a random number. If, for example, that function returns a number from 0 to 100, it will return 0 around 1% of the time. When that condition is met, we increase the counter by 100.
Why should we be concerned with this? Well, when working with large amounts of data or large numbers of users, the impact on performance of write operations can get to be large too. The more you scale up, the greater that impact is too and at scale, that's often your most important consideration. By reducing writes and reducing resources for data that doesn't need to be "perfect," it can lead to huge improvements in performance.
Sample Use Case
Population patterns are an example of the Approximation Pattern. An additional use case where we could use this pattern is for website views. Generally speaking, it isn't vital to know if 700,000 people visited the site, or 699,983. Therefore we could build into our application a counter and update it in the database when our thresholds are met.
This could have a tremendous reduction in the performance of the site. Spending time and resources on business critical writes of data makes sense. Spending them all on a page counter doesn't seem to be a great use of resources.
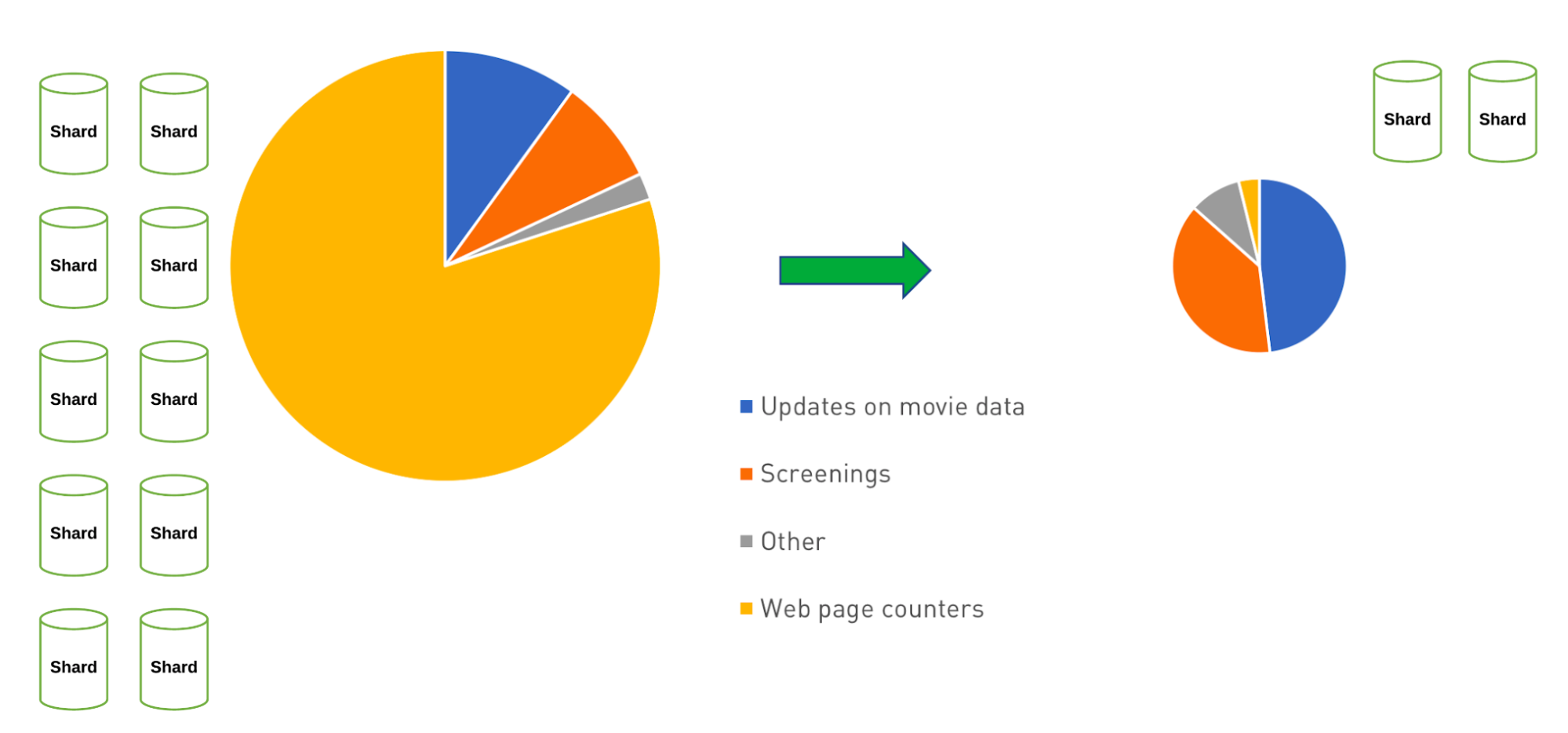
In the image above we see how we could use the Approximation Pattern and reduce not only writes for the counter operations, but we might also see a reduction in architecture complexity and cost by reducing those writes. This can lead to further savings beyond just the time for writing data. Similar to the Computed Pattern we explored earlier, it saves on overall CPU usage by not having to run calculations as frequently.
Conclusion
The Approximation Pattern is an excellent solution for applications that work with data that is difficult and/or expensive to compute and the accuracy of those numbers isn't mission critical. We can make fewer writes to the database increasing performance and still maintain statistically valid numbers. The cost of using this pattern, however, is that exact numbers aren't being represented and that the implementation must be done in the application itself.
The next post in this series will look at the Tree Pattern.
If you have questions, please leave comments below.
Previous Parts of Building with Patterns:
- The Polymorphic pattern
- The Attribute pattern
- The Bucket pattern
- The Outlier pattern
- The Computed pattern
- The Subset pattern
- The Extended Reference pattern